0 Comments
0 Shares
0 Reviews

Directory
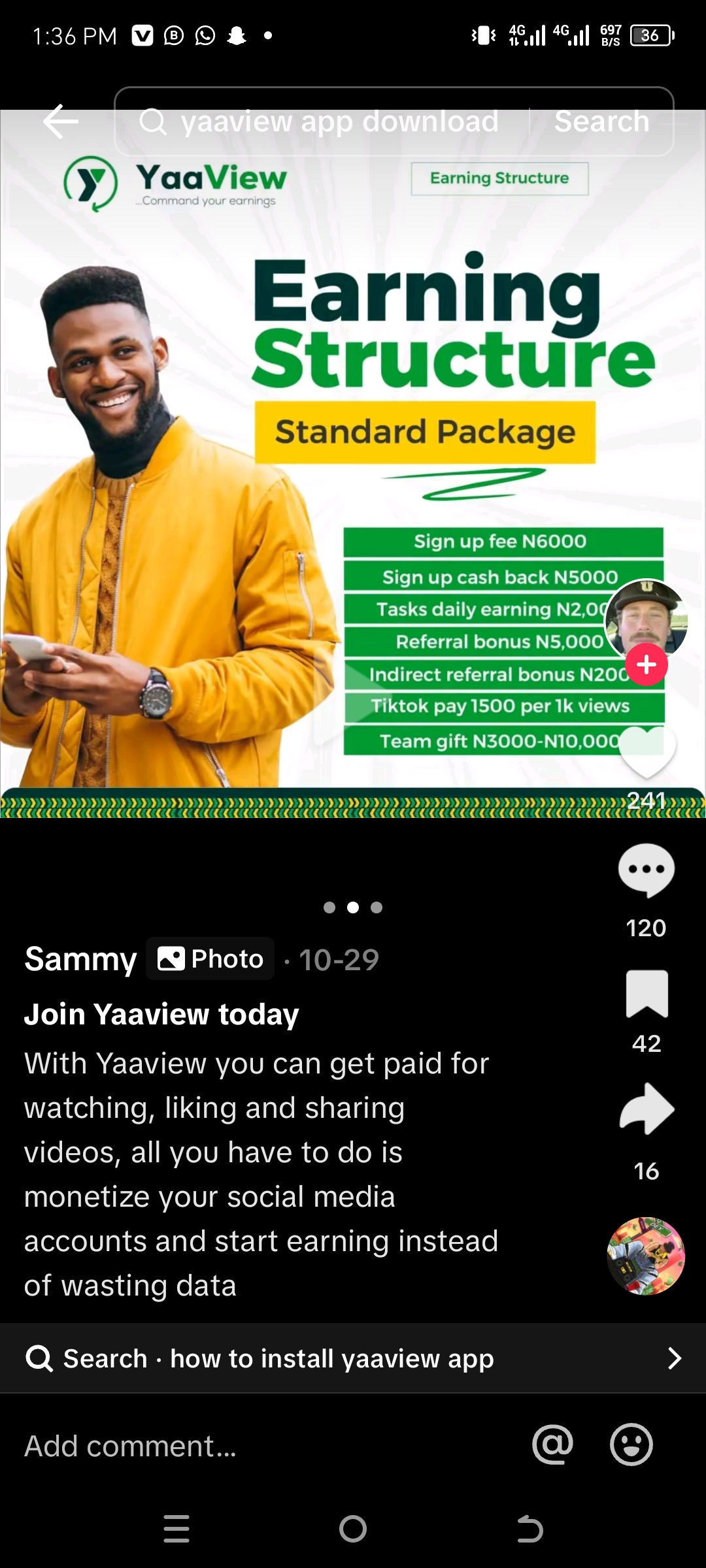
Genuine Profiles ONLY! Connect & Create. Be Rewarded. With Danloader, You Get to Find only genuine people, create genuine connections, and make genuine friends. You also earn rewards.
-
Please log in to like, share and comment!
-
-
-
-
-
Life is like a big merry go round, taking us back to the spot we've been. Please do good because life may recycle people you've hurt, and trust me, you won't be able to turn out the hands of time.Life is like a big merry go round, taking us back to the spot we've been. Please do good because life may recycle people you've hurt, and trust me, you won't be able to turn out the hands of time.0 Comments 0 Shares 0 Reviews
-
"No one in this world can ever love you more than your parents.""No one in this world can ever love you more than your parents."0 Comments 0 Shares 0 Reviews
-
You could give some people a drop of water and they'd still appreciate you. You could give other people the entire ocean and they'd still take you for granted.You could give some people a drop of water and they'd still appreciate you. You could give other people the entire ocean and they'd still take you for granted.0 Comments 0 Shares 0 Reviews
-
-
Here are some types of friends you may need to be careful with:
1. *Gossipers*: Friends who spread rumors or reveal your personal secrets.
2. *Toxic supporters*: Friends who encourage harmful behaviors or negative attitudes.
3. *Users*: Friends who only reach out when they need something, but aren't there for you in return.
4. *Manipulators*: Friends who try to control or influence your decisions for their own gain.
5. *Enablers*: Friends who enable harmful habits or behaviors, rather than encouraging positive change.
6. *Fake friends*: Friends who pretend to be something they're not, or who only care about appearances.
7. *Competitors*: Friends who turn everything into a competition, causing stress and tension.
8. *Emotional vampires*: Friends who drain your energy with constant negativity or drama.
9. *Liability friends*: Friends who consistently make poor decisions that may put you in difficult situations.
10. *Unreliable friends*: Friends who consistently flake or don't follow through on commitments.
Remember, it's important to surround yourself with positive, supportive friends who uplift and inspire you!Here are some types of friends you may need to be careful with: 1. *Gossipers*: Friends who spread rumors or reveal your personal secrets. 2. *Toxic supporters*: Friends who encourage harmful behaviors or negative attitudes. 3. *Users*: Friends who only reach out when they need something, but aren't there for you in return. 4. *Manipulators*: Friends who try to control or influence your decisions for their own gain. 5. *Enablers*: Friends who enable harmful habits or behaviors, rather than encouraging positive change. 6. *Fake friends*: Friends who pretend to be something they're not, or who only care about appearances. 7. *Competitors*: Friends who turn everything into a competition, causing stress and tension. 8. *Emotional vampires*: Friends who drain your energy with constant negativity or drama. 9. *Liability friends*: Friends who consistently make poor decisions that may put you in difficult situations. 10. *Unreliable friends*: Friends who consistently flake or don't follow through on commitments. Remember, it's important to surround yourself with positive, supportive friends who uplift and inspire you!0 Comments 0 Shares 0 Reviews
Sponsored
Sponsored
Sponsored
Sponsored
Sponsored